JDK1.8中红黑树的调整

红黑树

• 红黑树的五个性质
  • 每个结点要么为红色要么为黑色
  • 根节点为黑色
  • 叶子结点(指null)为黑色
  • 红色结点的子节点必为黑色
  • 一个节点到叶子节点的任一路径黑色结点的个数相同
• 红黑树的性能
  • 插入的时间复杂度：O(log n)
  • 查找的时间复杂度：O(log n)

源码解析

• 摘自 HashMap 中静态内部类 TreeNode 的 balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) 方法。其中，root 为红黑树的根节点，x 为刚按照二叉搜索树规则插入的结点。

  static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) {
    // 将刚插入的结点颜色赋为红色
    x.red = true;
    for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
        // 若结点的父结点为空，说明刚插入的结点就是根结点，将其重新赋为黑色并返回
        if ((xp = x.parent) == null) {
            x.red = false;
            return x;
        }
        // 若结点的父结点为黑色 或 父结点的父结点为空，则颜色与位置均不用改变，返回 root [1]
        else if (!xp.red || (xpp = xp.parent) == null)
            return root;
        // 函数进行到这里父结点为红色
        // 若父结点是爷结点的左结点
        if (xp == (xppl = xpp.left)) {
            // 若叔结点不为空 且 叔结点为红色
            if ((xppr = xpp.right) != null && xppr.red) {
                // 父结点和叔结点赋为黑色
                xppr.red = false;
                xp.red = false;
                // 爷结点赋为红色
                xpp.red = true;
                // 将爷结点赋给引用x
                x = xpp;
            }
            // 否则：叔结点为空 或 叔结点为黑色
            else {
                // 若 x 为右结点
                if (x == xp.right) {
                    // 左旋父结点
                    root = rotateLeft(root, x = xp);
                    // 旋转后父变子、子变父 x = xp 还是子，xp = x.parent还是父
                    // 给爷结点赋值
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                // 若父结点不为空
                if (xp != null) {
                    // 父结点赋为黑色
                    xp.red = false;
                    // 若爷结点不为空
                    if (xpp != null) {
                        // 爷结点赋为红色并对爷结点进行右旋
                        xpp.red = true;
                        root = rotateRight(root, xpp);
                    }
                }
            }
        }
        // 若父结点是爷结点的右结点
        else {
            // 若叔结点不为空 且 叔结点为红色
            if (xppl != null && xppl.red) {
                // 叔结点和父结点赋为黑色
                xppl.red = false;
                xp.red = false;
                // 爷结点赋为红色
                xpp.red = true;
                // 将爷结点赋给引用x
                x = xpp;
            }
            // 否则：叔结点为空 或 叔结点为黑色
            else {
                // 若 x 为左结点
                if (x == xp.left) {
                    // 右旋父结点
                    root = rotateRight(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                // 若父结点不为空
                if (xp != null) {
                    // 父结点赋为黑色
                    xp.red = false;
                    // 若爷结点不为空
                    if (xpp != null) {
                        // 爷结点赋为红色并对爷结点进行右旋
                        xpp.red = true;
                        root = rotateLeft(root, xpp);
                    }
                }
            }
        }
    }
  }
  

• 对 p 结点进行左旋

  static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p) {
    TreeNode<K,V> r, pp, rl;
    if (p != null && (r = p.right) != null) {
        if ((rl = p.right = r.left) != null)
            rl.parent = p;
        if ((pp = r.parent = p.parent) == null)
            (root = r).red = false;
        else if (pp.left == p)
            pp.left = r;
        else
            pp.right = r;
        r.left = p;
        p.parent = r;
    }
    return root;
  }
  

• 对 p 结点进行右旋

  static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p) {
    TreeNode<K,V> l, pp, lr;
    if (p != null && (l = p.left) != null) {
        if ((lr = p.left = l.right) != null)
            lr.parent = p;
        if ((pp = l.parent = p.parent) == null)
            (root = l).red = false;
        else if (pp.right == p)
            pp.right = l;
        else
            pp.left = l;
        l.right = p;
        p.parent = l;
    }
    return root;
  }
  

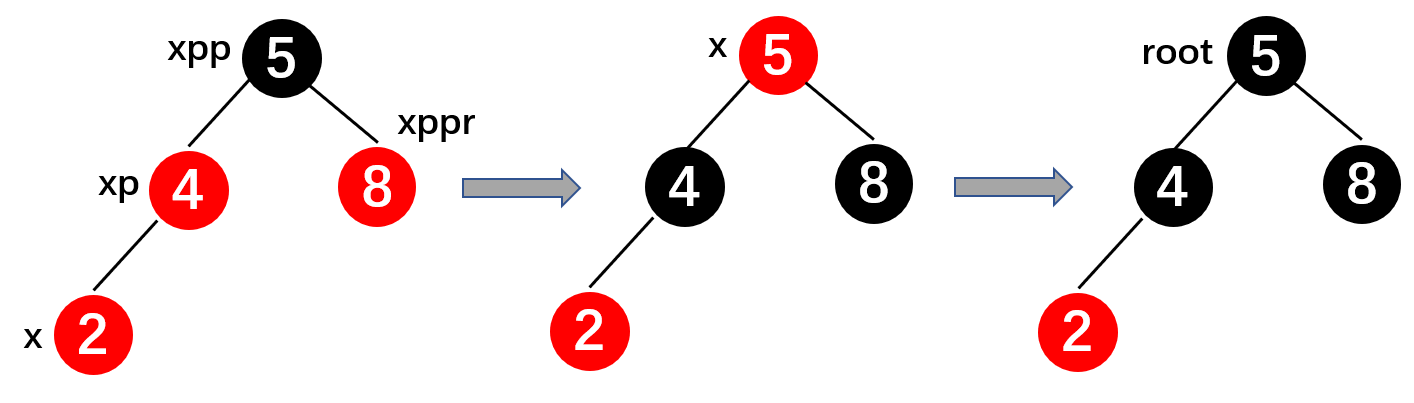
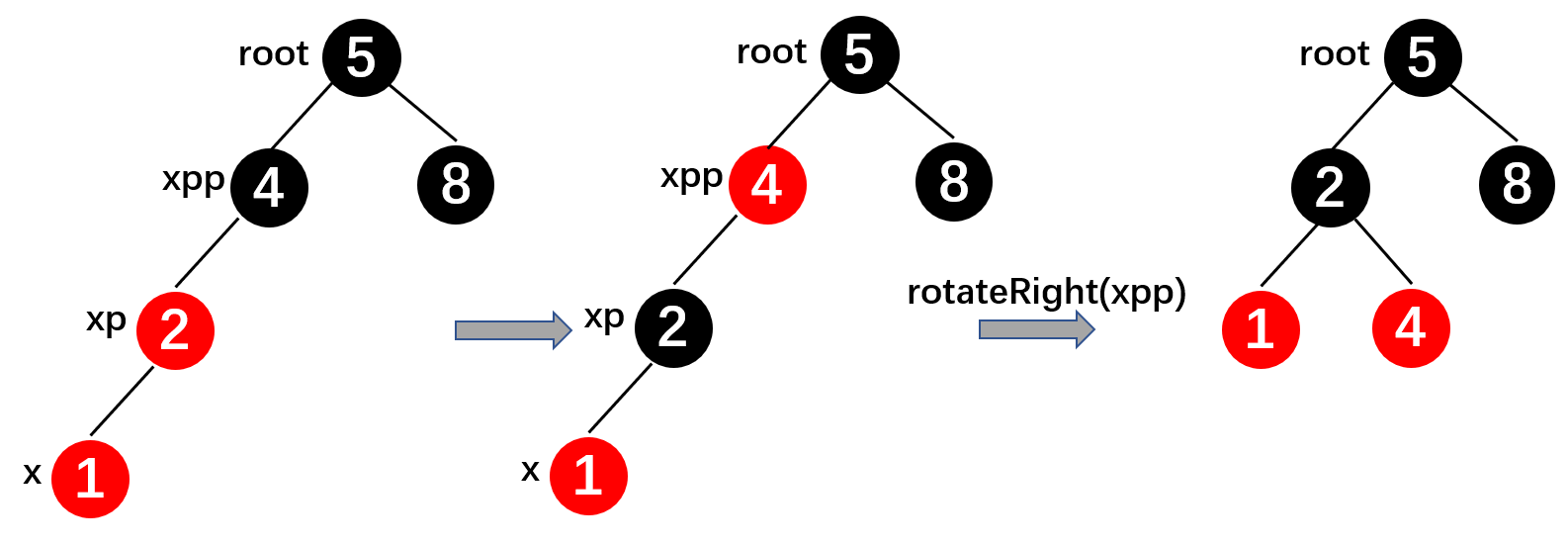
示意图