36 - 有效的数独

题目描述

判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

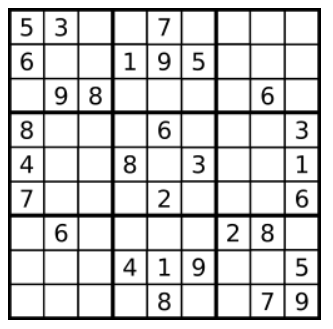
上图是一个部分填充的有效的数独。

数独部分空格内已填入了数字，空白格用 ’.’ 表示。

示例 1:

输入:  
[  
  ["5","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]  
]  
输出: true  

示例 2:

输入:  
[  
  ["8","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]  
]  
输出: false  
解释: 除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。  

说明:

• 一个有效的数独（部分已被填充）不一定是可解的。
• 只需要根据以上规则，验证已经填入的数字是否有效即可。
• 给定数独序列只包含数字 1-9 和字符 ’.’ 。
• 给定数独永远是 9x9 形式的。

链接：https://leetcode-cn.com/problems/valid-sudoku

题解

class Solution {
    public boolean isValidSudoku(char[][] board) {
        HashSet<Character>[] hsRow = new HashSet[9];
        HashSet<Character>[] hsCol = new HashSet[9];
        HashSet<Character>[] hsGrid = new HashSet[9];
        for(int i = 0; i < 9; i++) {
            hsRow[i] = new HashSet<>();
            hsCol[i] = new HashSet<>();
            hsGrid[i] = new HashSet<>();
        }
        for(int row = 0; row < 9; row++) {
            for(int col = 0; col < 9; col++) {
                char c = board[row][col];
                if(c == '.') {
                    continue;
                }
                if(hsRow[row].contains(c) || hsCol[col].contains(c) ||
                hsGrid[(row / 3) * 3 + col / 3].contains(c)) {
                    return false;
                }
                hsRow[row].add(c);
                hsCol[col].add(c);
                hsGrid[(row / 3) * 3 + col / 3].add(c);
            }
        }
        return true;
    }
}

返回